Original: http://staff.um.edu.mt/jskl1/dp/th.html
Jaroslav Sklenar, 30. oktoober 2007
Sissejuhatus
Hanoi torn(id) on tuntud mäng (pusle), mida tavaliselt kasutatakse rekursiooni jõu selgitamiseks ja demonstreerimiseks. Seal on väga palju veebisaite, mis sellega tegelevad. Mõnda paljudest mainimiseks võite külastada näiteks:
http://en.wikipedia.org/wiki/Tower_of_Hanoi
http://www.cut-the-knot.org/recurrence/hanoi.shtml
http://mathworld.wolfram.com/TowerofHanoi.html
ja paljud teised. Seda probleemi saab kasutada ka dünaamilise programmeerimise võimsuse demonstreerimiseks. Lisateabe saamiseks lugege Moshe Sniedovitši artiklit aadressil http://archive.ite.journal.informs.org/Vol3No1/Sniedovich/, kus lühima lahenduse pikkuse ja ka peaaegu ignoreeritud pikkuse leidmiseks on kasutatud dünaamilist programmeerimist. pikim lahendus (ja palju muud). Siin kasutame dünaamilise programmeerimise lähenemisviisi, et leida probleemile erinevaid lahendusi.
Olen ise selle tulemuseni jõudnud, kuid arvan, et ma pole esimene. Palun andke mulle teada kõigist allikatest, kus see valem on avaldatud. Mul on hea meel seda tsiteerida.
Teooria
Eeldan siinkohal, et lugeja on probleemiga tuttav, seega lihtsalt lühike kokkuvõte:
Neid kolme platvormi (poolust) nimetatakse L (vasakul), C (keskel) ja R (paremal).
Torn on kettade (rõngaste) kogum, mis asetatakse üksteise peale nii, et alati asetatakse väiksem ketas suuremale. Esialgu torni kõrgus n valmistatud kettaid 1…n suurendada suurus, kus 1 on top väikseim ketas, asub platvormi L.
Reeglid: ketaste teisaldamisel peame järgima järgmisi reegleid:
– korraga saab teisaldada ainult ühte ketast
– ketta võib asetada kas tühjale platvormile või suuremale kettale.
Probleem: tahame viia ketastest 1…n tehtud torni platvormilt L platvormile R, järgides reegleid.
Riigi mängu on antud kolme üksteist välistavad komplekti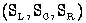 
selline, et 
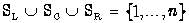. Teostatav seisund on selline, kuhu pääseb reegleid järgides.
See tagab ka selle, et need komplektid on kas tornid või võivad olla tühjad. Algseisund on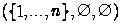 
, lõppseis on 
.
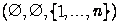Lahendus on käikude jada (alternatiivina nende käikude poolt genereeritud olekute jada), mis lahendab ülaltoodud probleemi reegleid järgides. Vaatleme ainult tsükliteta lahendusi, kus iga olek ilmub enamasti üks kord.
Olgu F(n,a,b,c) n-kõrguse torni teisaldamise platvormilt a platvormile b erinevate platvormide c lahenduse lahendamise lahenduste koguarv. Kuna reeglite osas pole platvormide vahel erinevusi, võime lühidalt kasutada F (n).
Teoreem: F (n) saab arvutada rekursiivse valemi abil
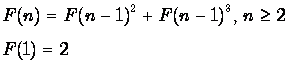
Tõestus: n = 1 korral on tsükliteta selgelt kaks lahendust: liigutage ketast L-st R-ni või liigutage ketast L-st C-ni ja seejärel C-st R-ni. Nüüd eeldame 
. Lõppseisundi saavutamiseks tuleb suurim ketas n viia punktist L R-ni. Seda saab teha (alati ilma tsükliteta) kahel erineval viisil, mida käsitleme eraldi.
1) Liigutage torni (n-1) L-st C-ni, liigutage ketast n L-st R-ni, liigutage torni (n-1) C-st R-ni. Torni (n-1) liigutamisel L-C on F(n-1) erinevad lahendused, torni (n-1) teisaldamisel C-st R on ka F (n-1) erinevad lahendused. Need kaks kõrguse (n-1) torni käiku on sõltumatud, nii et esimese juhtumi tulemuseks on F(n-1)2 erinevad lahendused.
2) Liigutage torni (n-1) L-st R-ni, liigutage ketast n L-st C-ni, liigutage torni (n-1) R-st L-ni, liigutage ketast n C-st R-ni, liigutage torni (n-1) L-st R-ni. Näeme, et tornis on kolm iseseisvat käiku (n-1), seega on antud juhul erinevate lahenduste koguarv F(n-1)3.
Kuna juhtumid 1) ja 2) on teineteist välistavad, on meil teoreemi valemi abil antud erinevate lahenduste koguarv.
Legendid
Prantsuse matemaatiku Edouard Lucase poolt 1883. aastal leiutas legendi ilmselt nullist:
“Legendi kohaselt on rühm idapoolseid munkasid kolme torni hoidjad, millel istuvad 64 kuldrõngast. Algselt olid kõik 64 rõngast virnastatud ühele tornile, kusjuures iga rõngas oli väiksem kui all olev. Mungad peavad kolima rõngad esimesest tornist kolmandasse torni ükshaaval, kuid mitte kunagi liigutades suuremat rõngast väiksema peale. Kui 64 rõngast on kõik ära kolitud, saab maailm otsa.”
(Lisateavet leiate lehelt http://hanoitower.mkolar.org, kust legend on võetud).
On hästi teada, et n-torni mängu optimaalne lahendus võtab 2n-1 käiku. Eeldades, et üks käik võtab 1 sekundi, jõuame pärast lihtsat arvutamist tulemuseni, et lahendus n = 64 võtab umbes 585×109 aastat.
Pakume veel ühte legendi:
„Võtke ainult 5 rõngast ja proovige kõiki võimalikke lahendusi. Siis saab Universum otsa”.
Kui võtame (ebareaalse) eelduse, et iga lahendus võtab keskmiselt (neil on erinevad pikkused) vaid 1 sekund, kulub nende kõigi proovimiseks umbes 89.67×1020 aastat. Piisavalt paljudele suurtele paugudele aega.
Veel üks legend:
„Võtke ainult 4 rõngast ja laske igal inimesel Maa peal mängu erineval viisil lahendada. Kui kõiki erinevaid lahendusi kasutatakse, saab universum otsa.”
Varem polnud Universumil üldse lõppu, kuid nüüd on see muutunud. Siiski on meil iga inimese jaoks peaaegu üks lahendus.
Tulemused
Torni kõrguse suurendamiseks on esitatud mitu lahendust:
F(1) = 2
F(2) = 12
F(3) = 1872
F(4) = 6,563,711,232
F(5) ≈ 2.827798101718050e+029
Allpool on toodud kõik lahendused tornide kõrgusele 1,2 ja 3 (väljavõte). Igas reas on üks number, mis algab selle numbriga. Tühikutega eraldatud käikude vorming on järgmine:
kAB
kus k on ketta number, mille liigutame platvormilt A platvormile B. Pange tähele, et esimene lahendus on lühim, 2n-1 käiguga, viimane lahendus on pikim, 3n-1 käiguga.
1 (torni kõrgus)
2 (loodud lahenduste arv)
1 1LR
2 1LC 1CR
2 (torni kõrgus)
12 (loodud lahenduste arv)
1 1LC 2LR 1CR
2 1LC 2LR 1CL 1LR
3 1LR 1RC 2LR 1CR
4 1LR 1RC 2LR 1CL 1LR
5 1LR 2LC 1RL 2CR 1LR
6 1LR 2LC 1RL 2CR 1LC 1CR
7 1LR 2LC 1RC 1CL 2CR 1LR
8 1LR 2LC 1RC 1CL 2CR 1LC 1CR
9 1LC 1CR 2LC 1RL 2CR 1LR
10 1LC 1CR 2LC 1RL 2CR 1LC 1CR
11 1LC 1CR 2LC 1RC 1CL 2CR 1LR
12 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR
3 (torni kõrgus)
1872 (loodud lahenduste arv)
1 1LR 2LC 1RC 3LR 1CL 2CR 1LR
2 1LR 2LC 1RC 3LR 1CL 2CR 1LC 1CR
3 1LR 2LC 1RC 3LR 1CR 1RL 2CR 1LR
4 1LR 2LC 1RC 3LR 1CR 1RL 2CR 1LC 1CR
5 1LR 2LC 1RC 3LR 1CR 2CL 1RC 2LR 1CR
6 1LR 2LC 1RC 3LR 1CR 2CL 1RC 2LR 1CL 1LR
7 1LR 2LC 1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CR
8 1LR 2LC 1RC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR
9 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CR
10 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RC 2LR 1CL 1LR
11 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CR
12 1LR 2LC 1RC 3LR 1CL 1LR 2CL 1RL 1LC 2LR 1CL 1LR
13 1LR 2LC 1RL 1LC 3LR 1CL 2CR 1LR
14 1LR 2LC 1RL 1LC 3LR 1CL 2CR 1LC 1CR
15 1LR 2LC 1RL 1LC 3LR 1CR 1RL 2CR 1LR
16 1LR 2LC 1RL 1LC 3LR 1CR 1RL 2CR 1LC 1CR
17 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CR
18 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RC 2LR 1CL 1LR
19 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CR
20 1LR 2LC 1RL 1LC 3LR 1CR 2CL 1RL 1LC 2LR 1CL 1LR
. . .
1865 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR 2LC 1RL 2CR 1LR
1866 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR 2LC 1RL 2CR 1LC 1CR
1867 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR 2LC 1RC 1CL 2CR 1LR
1868 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LR 2LC 1RC 1CL 2CR 1LC 1CR
1869 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC 1CR 2LC 1RL 2CR 1LR
1870 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC 1CR 2LC 1RL 2CR 1LC 1CR
1871 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC 1CR 2LC 1RC 1CL 2CR 1LR
1872 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR 3LC 1RC 1CL 2RC 1LC 1CR 2CL 1RC 1CL
3CR 1LC 1CR 2LC 1RC 1CL 2CR 1LC 1CR
3. kõrguse torni jaoks saate alla laadida tekstifaili kõigi lahendustega.
Erinevate lahenduste arv isegi väikeste tornide jaoks on muljetavaldav. Valemi kontrollimiseks, mille olen kirjutanud programmis Turbo Pascal 7, mis genereerib ülaltoodud vormingus tekstifailis olevad lahendused, kontrollige, kas kõik lahendused on erinevad, ja simuleerige neid, kas need on õiged. Neid saab kasutada ka käsitsi loodud lahenduste jaoks. Kui soovite, võite need programmid alla laadida. Kõik peaks olema selge allikafailide kommentaaridest.
