Arhiimede kallistused ja Egiptuse fraktsioonid

Original: http://math.ucr.edu/home/baez/egyptian.html

John Baez

5. veebruar 2012

Sellest ajast olin laps, ma olen armastanud Archimedean paanimist lennuk: see tähendab, paanimist regulaarne hulknurga kus kõik serva pikkusega on sama ja iga tipu välja samasugused. Siin on minu lemmik:

Neid on ka 11, neist kaks on üksteise peegelpildid. Aga kuidas me seda teame? Kuidas neid kõiki loetleda ja olla kindlad, et me pole ühtegi välja jätnud?

Tavalise k-küljega polügooni sisenurk on ilmselge

π - 2 π/ k

kuna see on natuke alla 180 kraadi või $π,$ ja kui palju? – noh, $1 / k$ korda täispööret või 2π $2 π .$ But these $π$ muutuvad tüütuks: kergem on öelda “täielik pööre” kui kirjutada 2π $2 π .$ Siis võime öelda, et sisenurk on

1/2−1/k

korda täispööre.

Oletame nüüd, et meil on Archimedeani plaatimine kuhu n hulknurgad kohtuvad: üks koos k₁sides, one with k₂ hulknurgad kohtuvad: üks koos $k_{n}$ $k_{n}$

(1/2 − 1/k₁) + ⋯ + (1/2 − 1/ $k_{n}$ ) = 1

või

n/2 − 1/k₁− ⋯ − 1/ $k_{n}$ = 1

või

1/k₁+ ⋯ + 1/ $k_{n}$ = n/2 − 1

Niisiis: Archimedeani plaatimise saamiseks on vaja n täisarvu, mille vastandväärtused moodustavad ühe vähem kui n/2.

Selliste numbrite otsimine on imelik väike matemaatika mõistatus. Egiptlastele meeldis numbrite kirjutamine kui vastastikune summa, nii et nad oleksid võinud seda mängu nautida, kui nad oleksid seda teadnud. Plaatimine, mida ma teile näitasin, pärineb sellest lahendusest:

1/4 + 1/6 + 1/12 = 3/2 − 1

kuna sellel on igas tipus kokku kolmnurkne ristkülik: 4-poolne, 6-poolne ja 12-külgne.

Siin on veel üks lahendus:

1/3 + 1/4 + 1/4 + 1/6 = 4/2 − 1

See annab meile selle plaatimise:

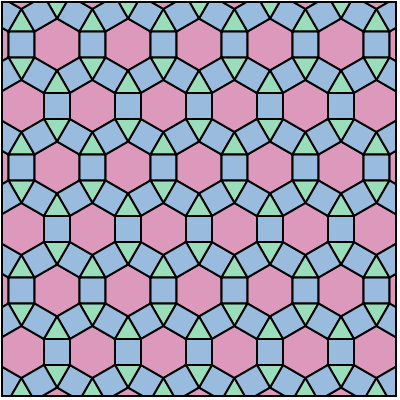
Hmm, nüüd ma arvan see üks on minu lemmik, sest mu silm näeb seda kui kamp seotud 12-sided polügoonide, omamoodi nagu kett mail. Erinevad paanimist teha mu silmad liiguvad üle neid erinevalt, ja see üks on väga meeldiv tunne.

Siin on veel üks lahendus:

1/3 + 1/3 + 1/3 + 1/3 + 1/6 = 5/2 − 1

See annab kaks Archimedeani kallutust, mis on üksteise peegelpildid!

Muidugi sõltub see, kas loete neid kahte erinevat Archimedeani kallutust või ainult ühte, sellest, milliseid reegleid valite. Ja muide, tavaliselt ei öelda, et plaatimine on Archimedean, kui kõik polügoonid on ühesugused, näiteks:

Nad asemel öelda, et see on regulaarne. Kui kaasaegne matemaatikud olid leiutas selle teema, me tahaks öelda regulaarne paanimist erijuhtum archimedese paanimist – kuid see matemaatika on kõik väga vana ja toona matemaatikud töödeldud erijuhtude ei kuulu üldise juhul. Näiteks kreeklased ei pidanud isegi number 1 olema number!

Nii et siin on lõbus puzzle: klassifitseerida Archimedese paanimist! For starterid, teil on vaja leida kõik võimalused saada $n$ täisarve kelle reciprocals lisada kuni üks vähem kui $n / 2$ . See kõlab raske, kuid õnneks on see ilmselge, et

n ≤ 6

kuna võrdkülgsel kolmnurgal on väikseim sisenurk, mis tahes tavalisel hulknurgal, ja neist mahub tipu ümber ainult 6. Kui natuke järele mõelda, näete, et see loob mõistatuse lõpliku otsinguni.

Kuid peate olema ettevaatlik, kuna on olemas mõned lahendused, mis ei anna Archimedeani kallutusi. Nagu tavaliselt, põhjustab number 5 probleeme. Meil on

1/5 + 1/5 + 1/10 = 3/2 − 1

kuid lennukit ei saa mingil viisil plaadistada, nii et 2 tipu viisnurka ja 1 tavalist dekagooni kohtuvad igas tipus! Tundub, et Kepler on proovinud; siin on pilt tema raamatust Harmoonikud Eelnevad:

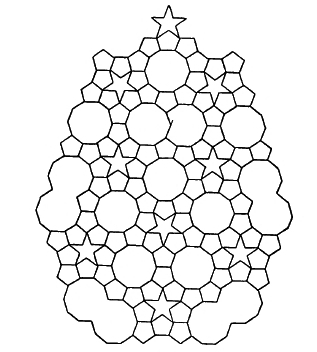
See toimib ilusti ühe tipu, kuid mitte plaatimistööd kogu lennukiga. Et päästa päev tal lisada mõned tähed, ja mõned decagons kattuvad! Islami plaatimistööd kunstnikud ja hiljem Penrose, läks edasi selles suunas.

Kui te jänni selle puzzle, saate leida vastus siin:

• Michal Krížek, Jakub Šolc ja Alena Šolcová, Kas kristallvõre kellel viiekordne sümmeetria?, AMS teatised 59 (jaanuar 2012), 22-30.

• Kombinatsioonid korrapärase hulknurga kuju, mida saab kokku tipuga, Wikipedia.

Mitte piisavalt?

Lühidalt, kõik Archimedean paanimist lennuk tuleneda leida $n$ täisarve kelle reciprocals Kokkuvõttes et n/2 − 1 $n / 2 - 1.$ Aga mis siis, kui kogu ei piisa? Ära tunne end halvasti: võite ikka plaatimistööd kohta hüperboolse lennuk. Näiteks,

1/7 + 1/7 + 1/7 < 3/2 − 1

nii et te ei saa plaati plaadida nii, et iga nurga all on kolm heptagoni, kuid hüperboolse tasapinna plaatimine on siiski järgmine:

mis juhtub olema seotud imeline asi nimega Klein quartic kõver.

Te ei pea alati võita… aga mõnikord sa teed, nii et mäng on väärt mängimist. Näiteks,

1/3 + 1/3 + 1/3 + 1/3 + 1/3 + 1/4 < 6/2 − 1

nii et sa on võimalus juures plaatimistööd hüperboolse lennuk, kus viie võrdkülgse kolmnurga ja ruudu kohtuvad igal tipu. Ja sel juhul, siis õnne välja:

Rohkem ilusaid pilte nagu need, vt:

• Ühtsed paanimist sisse hüperboolse lennuk, Wikipedia.

• Don Hatch, Hüperboolne tesselations.

Liiga palju?

Samamoodi, kui sul $n$ reciprocals et lisada kuni rohkem kui n/2 − 1, sul on võimalus võita plaatimistööd sfääri. Näiteks,

1/3 + 1/3 + 1/3 + 1/3 + 1/5 > 5/2 − 1

ja sel juhul me õnne välja ja saada tölväistä dodecahedron. Ma arvasin, et see oli ebaviisakas tölväistä sidususele, kuid ilmselt mitte:

Need paanimist kera on tehniliselt nimetatakse Archimedean kuivainete ja (kui kõik polügoonide on samad) Platon tahke aine . Neist ainult Tölväistä dodecahedron ja “Tölväistä kuubik” erinevad nende peegelpildid.

Kasvataja kraami

Lühidalt, lisades kuni reciprocals täisarve on seotud Archimedean paanimist lennuk, sfääri ja hüperboolse lennukiga. Aga see on ka, kuidas egiptlased oleks kirjutada fraktsioonid! Tegelikult nad isegi nõudis, et kõik reciprocals olla erinevad, nii et selle asemel kirjalikult 2/3 kui $\frac{1}{3} + \frac{1}{3}$ , nad kirjutaksid $\frac{1}{2} + \frac{1}{6} .$

See on täitanud süsteem – kahtlemata on see, miks King Tut suri nii noor. Aga unustada piirang, et reciprocals olla erinev: see rumal. Kui saate näidata, et iga $n > 1$ arvu $4 / n$ võib kirjutada 1/a + 1/b + 1/c eest täisarve a, b, c, saate kuulsaks! Seni inimesed on “ainult” näidatud see kehtib n kuni sada triljonit:

• Erdös-Straus oletustele, Wikipedia.

Niisiis, kas te saate teha parem! Aga vähem stressi aktiivsus võib olla loe Egiptuse fraktsioonid siin:

• John Baez, 42.

Nagu pealkiri soovitada, see keskendub erilist magic tulenevad selle võrrandi:

1/2 + 1/3 + 1/7 + 1/42 = 1

Kuid lõpu lähedal on mõned asjad Egiptuse fraktsioonide kohta üldiselt, see on siinse lehe omamoodi jätk.
Ja pärast seda saate lugeda Egiptuse fraktsioonide, kallutuste ja ADE klassifikatsioonide kohta siit:

• John Baez, Selle nädala leiab Matemaatiline füüsika (Nädala 182).

See ainult satub “Platon” või “tavalisi” paanimist, mitte üldisem “Archimedean” või “semiregular” ones ma räägin täna – nii aritmeetiline töötab natuke teistmoodi.

Teises suunas, kolleeg Julie Bergner rääkis, kuidas nad Egiptuse fraktsioonid kuvata uuring “groupoid kardinaalsusega”:

• Julie Bergner Groupoids ja Egiptuse fraktsioonid.

Seega, kui keegi kasutab Egiptuse fraktsioonid palju enam, nad on omamoodi jube hauataguses elus. Lisateavet mida egiptlased tegelikult tegi, proovige neid:

• Ron Knott, Egiptuse fraktsioonid.

• Egiptuse fraktsioonid, Wikipedia.